本文共 42496 字,大约阅读时间需要 141 分钟。
自学javase回顾(5/10)
1、接口interface
2、匿名内部类InnerClass
3、包package和导包import
4、Object类(API)
1、接口interface
一、先用一张图来让大家回顾之前面向对象知识点,并且预习后面接口和内部类
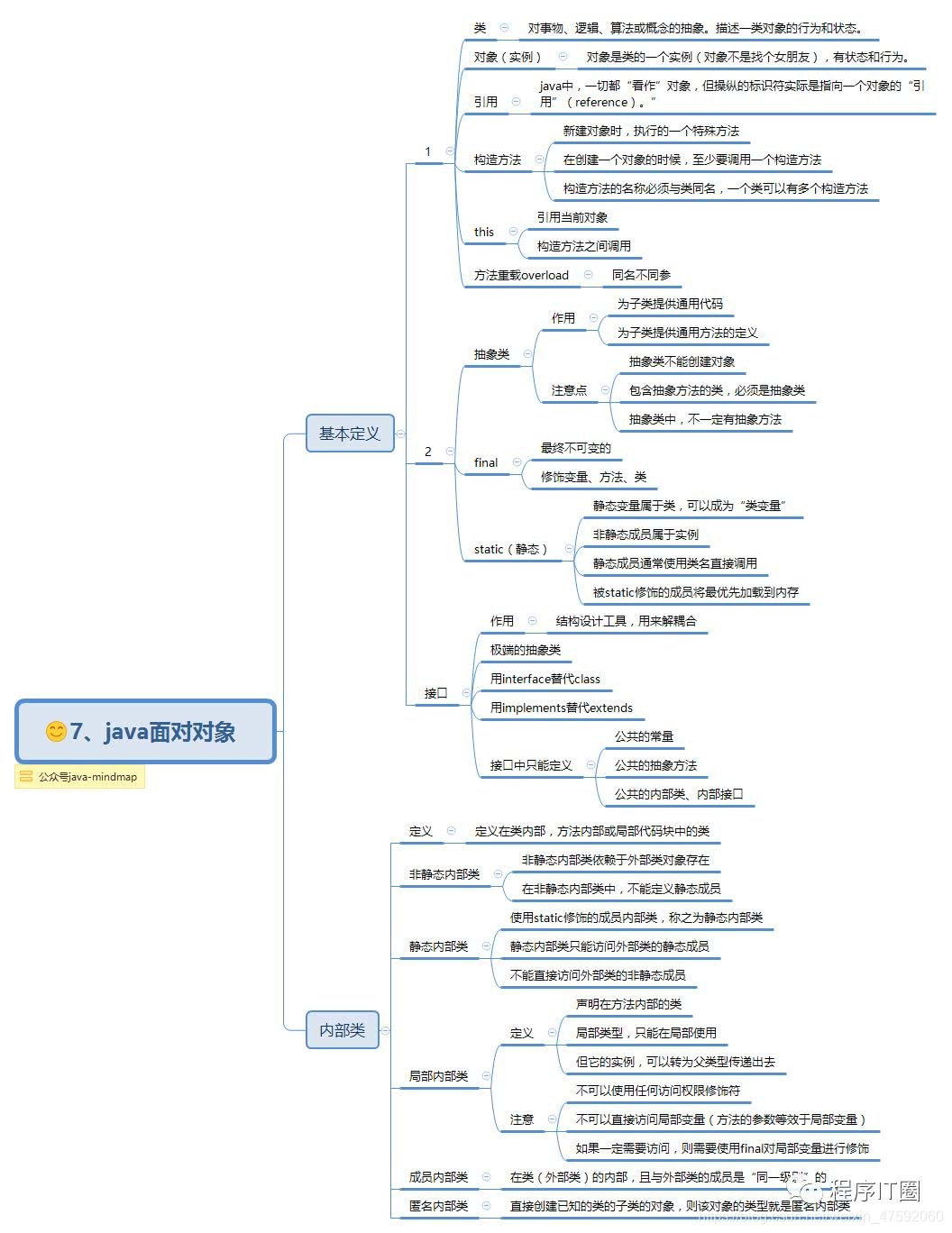
二、看完图咋们正式开始学接口interface
1、接口概念?(接口就是特殊的抽象类) ①接口和抽象类都是一种引用数据类型 ②通俗来讲:接口其实就像一个组成插件,给某个类去实现特殊功能(去插上一个翅膀插件),那么具体是利用多态让类实现某个接口功能。1、接口的注意点?
①接口不能被实例化,接口中没有构造函数的概念 ②接口之间可以多继承,但接口之间不能实现。(一类可以实现多个接口) ③如果一个类实现了接口,那么接口中所有的方法必须实现 ④class类可以同时extens父类 + implements 父接口(完美形态,既可以和父类多态又可以和接口多态,一脚踏两船)1、接口在开发中的意义和作用?(精华;解耦合,提扩展)
①简单来说:接口一方面解决 java 的单继承问题,同时还实现了强大的可插拔性 有了接口就有了——可插拔功能 ,可插拔扩展力强,耦合度低(可以给一个类插上可放音乐的功能,也可以把它拔了去换成可跳舞的功能,看具体业务需求)② 升华来说:面向接口编程使用多态,可以降低程序耦合度,提高程序扩展力,符合OCP开闭原则;(以后大的项目都是一个模块一个模块分割开的,大家各司其职,最后用各自的接口衔接上功能。分工明确的)
③而且接口使用多态后还可以做到具体行为具体分析:抽象类和接口都可以利用多态间接创建对象,只是后边的new不能是new他们自己,但可以new他们的实现类(必须是类,不能是抽象类和接口),
比如: 人们使用抽象类和接口只是为了说明要干什么事,而让他们的实现类去根据自己的需要去实现这些方法,比如说抽象父类或者接口定义一个eat()方法, 它并没有说这个方法具体方法体内容怎么做,比如羊就可以吃输出草,虎就可以输出吃肉,但是羊和虎都实现了这个吃的方法。从而做到具体行为具体分析2、接口语法结构:
(接口不能用class修饰了,完全抽象的) 接口结构;【修饰符列表】+interface+ 接口名{} 普通类结构;【修饰符列表】+class +类名{} 抽象类结构;【修饰符列表】+ abstract + class +类名{ 接口体(抽象方法和常量); }3、接口内部组成结构:
(不能有方法体,不能有方法体,不能有方法体!!!) ①全是常量。 (接口里可省public final static)+ 类型 +常量名 = 字面值(全部大写) ②全是抽象方法名。( 接口里可省public abstract )+返回值类型+ 方法名(参数列表); ③完全抽象的,不能有方法体和构造方法(抽象类有)。4、接口中在定义“抽象方法”的时候,public 和abstract 修饰符都可以省略。
public abstract int num(String name); ——》 int num(String name);5、接口中在定义“常量·”的时候, public final static 可以省略,
直接写成局部变量形式。但是语法规则还是遵守,即常量不可变不能二次赋值。6、一个非抽类去实现接口时抽象方法必须实现抽象方法。 1、必须实现抽象方法的原因:
① 抽象方法只能出现在抽象类(半抽半非抽)和 接口(全抽) ② 因此非抽象类implements实现单个或者多个“接口的”时候,必须把全部的接口的全部抽象方法“实现”化,即方法体内写括号就好了(因为接口全是抽象方法) 2、重写抽象方法的注意点: ③ 非抽象类只有在extends抽象类的抽象方法时,必须去掉abstract重写覆盖,不然无法继承并且报错。 ④如果是接口省略了public abstract,实现必须把public 补回去,再省略abstract。 public abstract void sum(无方法体);——》 public void sum() {有方法体}7、interface接口细节注意点:!!!!
③接口中所有的元素都是public修饰的,(都是公开的,和常量一样)。 因此在覆盖重写之后的子类方法也必须是public,因为覆盖重写之后的权限不能变低。这是覆盖的条件 ④覆盖重写之后的子类不能throws抛出更多的异常,只能更少。8、extends和implements关键字如何抉择去使用?
总结:(同种类用extends,异类叫实现用implements) 先来学习类和接口继承形式。 ①类和类之间只支持单继承(只能有一个爹父类),class B extends A{} ②接口和接口之间支持多继承,一个接口可以继承多个接口(可以多个爹)。 interface C1 extends A1,B1{} ③类和接口之间支持多实现,一个类可以实现多个接口(可以多个爹) 用implements class H implements E,F,G 因此进一步总结得出: 【1】 类和类相互之间用继承extends, class B extends A{} 只支持单继承 【2】接口和接口相互之间也用继承extends。 interface C1 extends A1,B1{} 单、多继承都支持 【3】 类和接口相互之间用实现implements(也可以看成是继承) class Math implements MyMath1{} 单、多继承都支持9、 类型和类型之间的关系如何抉择去使用
①、Cat is a Animal 。 但凡满足 is a 可以设置为“extends继承关系” class Cat extends Animal{} ②、f1 like a Foodmenu 但凡满足 like a (功能像) 可以设置为“implements实现关系” class ChineseCook implements FoodMenu 代表的是厨师的功能像个菜单一样,帮你实现菜名的具体做菜方法(从抽象到具体) (就跟媒介是一样的)司机像导航一样,帮你找路。老师像课本一样,教你知识。医生像药品一样,帮你治病。③、Customer has a FoodMenu 。但凡满足 has a 的在设置为“包含关系”(实例变量属性)。
特殊的Customer{ FoodMenu foodMenu; } 1、我有一个菜单(封装为顾客类的一个属性,为其所用),即是接口,也是引用,也是实例变量。 2、正常属性的String name;我有一个名字 int id 我有一个账号 }public class 接口基本语法 { public static void main(String[] args) { }}class MyClass1{ }//类只支持单继承类,但支持实现多个接口class MyClass2 extends MyClass1{ }class Myclass2 implements A,B,C{ }//接口支持多继承接口,可以有多个爹父接口。接口不能实现接口interface C extends A,B{ }interface A { }interface B{ }interface MyMath{ //接口内部具体语法接口。 public abstract int sum(String name); //正常的抽象方法写法 int num(String name); // 接口内简便的写法;public abstract 可以省略不写。 //void dosome(){方法体} //错误写法;直接报错,不能有方法体。 public final static double PI = 3.1415926; //正常常量 int PD = 111; // 接口内可省 public final static,但是一样不能二次赋值。} 三、子父接口之间也能实现多态向上向下转型
1、接口进阶语法(支持多继承)? ①(一台计算机有多个接口,一个连接主机,一个连接屏幕,一个连接鼠标键盘。。。等) ②因此一个类可以实现多个接口,这叫多实现,也叫多继承。弥补了java中class类单继承的缺陷2、多态向下强制转型的总分类?
前提:都要instanceof亲自鉴定,不然会抛出异常ClassCastException ①类和类之间(前提需要继承关系) 前提: 要instanceof保证强转后的类对象,是父类之前所指向的对象 ②接口和类之间(前提需要实现关系) 前提: 要instanceof保证强转后的类对象,是父接口之前所指向的对象 ③接口和接口转换(在没有继承关系下)也能进行转换 前提: 1、两个互转接口都要被同一子类son实现 2、还要instanceof保证强转后的Son类对象,是被转接口X之前所指向的对象,这样Y接口才能正常调Son的方法。 作用:(从X接口转换Y接口去调子类son的方法,因此一定都要被同一个子类实现,这样接口转换之后也可以正常多态调子类的方法)。public class 一个类可以实现多个接口 { public static void main(String[] args) { X x = new Son(); //向上转型多态间接创建对象 Y y = new Son(); Z z = new Son(); x.m1(); y.m2(); //不会报错,静动态就能绑定mw方法。 z.m3(); //②接口和类之间也能多态向下转型。(调用其他接口特有的方法) X x1 = new Son(); //先向上转,子变父,父类指向子类son对象 Son s1 = (Son)x1; //向下转型,父变子,前提保证父类x1之前向上转型所指向的对象就是强转后的对象,不然运行异常 //x1父亲指向的是son子类,然后x1父亲也是要强转的son子类,不会异常 //要做亲子鉴定 instanceof if (x1 instanceof Son) { //亲子鉴定 s1.son特有方法(); } X x2 = new Son(); //③接口和接口之前也能多态转型。(这叫接口转型,调用其他接口的特有方法) Y y2 = (Y)x2; //在没有继承关系下,接口X和接口Y之间也能强转。编译不会报错 //但是要注意,运行时可能会出现ClassCastException,因为前提要保证两个接口父类的多态儿子对象为同一对象(两接口都要被son所实现) //从 //也要做亲子鉴定 instanceof if (x2 instanceof Son){ //亲子鉴定 // 还要instanceof保证强转后的Son类对象,是被转接口X之前所指向的对象,这样Y接口才能正常调Son的方法。 y2.m2(); } System.out.println("000"); }}interface X{ void m1();}interface Y{ void m2();}interface Z{ void m3();}class Son implements X,Y,Z{ //普通类实现接口 public void m1(){ //抽象方法继承必须实现抽象方法 System.out.println("X接口的被X类实现了,多态调用了son的m1方法"); } public void m2() { System.out.println("Y接口的被son类实现了,多态调用了son的m2方法"); } public void m3() { System.out.println("Z接口的被son类实现了,多态调用了son的m3方法"); } public void son特有方法(){ System.out.println("son特有方法被实现了"); }}X接口的被X类实现了,多态调用了son的m1方法Y接口的被son类实现了,多态调用了son的m2方法Z接口的被son类实现了,多态调用了son的m3方法son特有方法被实现了Y接口的被son类实现了,多态调用了son的m2方法000 四、特殊使用(可以共存,先extends后implements)
【1】即class类可以同时extens父类 + implements 父接口(完美形态,既可以和父类多态又可以和接口多态,一脚踏两船)【2】接口+多态,面向接口编程,不要面向具体编程,降低耦合,提高扩展。
接口其实就像一个插件,给某个类去实现(去独自插上一个插件),用多态让类其实现某个特殊功能。 ①class Cat extends Animal implements Flyable 猫在继承父类的前提下,给猫独自去插上一个翅膀(插件),让猫可以飞 ②class Snake extends Animal 蛇只继承父类,没有插上翅膀接口,没有给予翅膀,因此无法实现飞翔这个功能extends和implements同时使用案例;(先继承后实现)
public class 接口进阶语法extends和implements同时使用 { public static void main(String[] args) { //用多态,间接创建接口对象,表面上Animal父类没起作用。 Flyable f1 = new Cat();//猫子类和接口多态 f1.fly(); Flyable f2 = new Pig();//猪子类和接口多态 f2.fly(); //虽然调用同一个方法,但执行的结果不同,这就是类和接口多态联用的面向接口编程。 Flyable f3 = new Fish(); f3.fly(); }}//父类动物class Animal{ }//翅膀接口 //可飞翔的接口插件(这里接口相当于是一对翅膀,可插可拔)。//接口名是组成插件,而接口内容通常提取的是行为动作(就是有了该接口插件可以干什么)interface Flyable{ void fly();}//子类Cat//Flyable是一个飞翔接口插件,相当于是一对翅膀,按在猫身上,让猫可以飞翔。class Cat extends Animal implements Flyable{ public void fly(){ //实现接口必须要加上public System.out.println("猫装上了翅膀可以起飞了"); }}//子类猪class Pig extends Animal implements Flyable{ public void fly(){ System.out.println("猪装上了翅膀可以起飞了"); }}//注意,就算没有直接继承+实现,也会有默认的Object类给予继承。 //class Fish extends Object implements Flyableclass Fish implements Flyable{ public void fly(){ System.out.println("我是飞鱼,装上了翅膀可以起飞了"); }}class Snake{ } 五、 总结抽象类和接口区别?
1、不同点: ①、抽象程度不同: 接口是完全抽象的(接口里面只有抽象方法,没有方法体也没构造方法)。 抽象类数半抽象的(类里面既可以有抽象方法,也可以有非抽象方法,有构造方法)。 ② 具体内容不同: 抽象类是半抽象的(包含抽象方法和非抽方法),有构造方法 接口是完全抽象的。(只有抽象方法和常量),无构造方法③灵活性不同
【1】一个类继承抽象类后,无法再次继承别的类。(java只支持类单继承) 【2】一个类实现一个接口后,还可以再次实现别的接口。(java支持类多实现) 【3】因此优先选择接口(因为继承抽象类后,此类将无法再继承,所以会丧失此类的灵活性)2、 相同点:
①由于都带有抽象性,因此接口和抽象类一样,无法直接实例化创建对象, MyMath1 m = new MyMath1(); 抽象类和接口创建对象都会报错 ②但是都可以和多态联用,去间接创建对象,让父类引用地址指向子类对象 MyMath1 m = new MyMath1(); //错误:(20, 12) java: MyMath1是抽象的; 无法实例化 MyMath1 m = new Math(); //只能和多态联用, 父类引用地址指向子类对象六、在继承和多态的前提下,我们程序员要学会:
【1】老铁们以后要多面向抽象和接口编程,使用多态,不要面向具体编程。降低耦合度,提高扩展度。 【2】 面向抽象编程(抽象父类和子类多态) 前提;非抽象类继承抽象类 class Bird extends (abstract)Animal 【3】面向接口编程(接口和子类多态) 前提;非抽先继承非抽,后实现接口 class Cat extends Animal implements Flyable{}【4】抽象类和接口都可以间接创建对象,只是后边的new不能是new他们自己,但可以new他们的实现类(必须是类,不能是抽象类和接口),
人们使用抽象类和接口只是为了说明要干什么事,而让他们的实现类去根据自己的需要去实现这些方法,比如说抽象父类或者接口定义一个eat()方法, 它并没有说这个方法具体方法体内容怎么做,比如羊就可以吃输出草,虎就可以输出吃肉,但是羊和虎都实现了这个吃的方法。从而做到具体行为具体分析接口和多态联合案例1:
public class 接口和多态的联用 { public static void main(String[] args) { // MyMath1 m = new MyMath1();//错误:(20, 12) java: MyMath1接口也是是抽象的; 无法实例化创建对象 MyMath1 m = new Math(); //只能和多态联用(间接创建对象),父类地址指向子类对象 //向上转型 System.out.println(m.num(30,20)); //引用调用num实例方法,并接受返回值。10 System.out.println(m.sum(30,20)); //引用调用sum实例方法,并接受返回值。50 }}interface MyMath1{ /* double PI = 3.1415926; //两个常量 int PD = 111;*/ int num(int a ,int b); //两个抽象方法,没有方法体 int sum(int a ,int b);}class Math implements MyMath1{ //类和接口之间叫实现 /*int num(int a, int b) { 错误:(42, 9) java: 正在尝试分配更低的访问权限; 以前为public 这里必须写public,覆盖重写的方法访问权限不能变低,可以更高。低权限不能访问高权限 return a+b; 接口父类的方法为public 只是省略了,但是非抽象类重写是不能省略的。只能在接口才能省略。 }*/ public int num(int a, int b) { //非抽象类继承抽象类也重写,非抽象类实现接口也要重写。 return a-b; } public int sum(int a, int b) { return a+b; }}1050 上面例子的升级版: (拆分为方法传参多态)
public class 接口和多态的联用 { public static void main(String[] args) { // MyMath1 m = new MyMath1();//错误:(20, 12) java: MyMath1接口也是是抽象的; 无法实例化创建对象 MyMath1 m = new Math(); //只能和多态联用(间接创建对象),父类地址指向子类对象 //先向上转型 Math math = (Math)m; //升级版,减少主方法代码,因此使用单独写一个order方法拆分步骤,在order里面实现计算功能 //再向下转型访问子类特有的oder方法 //这里不向下转型也行,在接口多写一个order方法即可。不当成子类特有方法,当成父类共有方法直接向上即可,看实际开发需求 math.order(new Math()); //下面实现接口和类多态 MyMath1 m1 = new Math(); }}interface MyMath1{ int num(int a ,int b); //两个抽象方法,没有方法体 int sum(int a ,int b);}class Math implements MyMath1{ //类和接口之间叫实现 public void order(MyMath1 m1){ //升级在这里实现接口和类的多态,减少主方法的代码。 System.out.println(num(30,20)); //进入方法求减 System.out.println(sum(30,20)); //进入方法求和 } public int num(int a, int b) { //非抽象类继承抽象类也重写,非抽象类实现接口也要重写。 return a-b; } public int sum(int a, int b) { return a+b; }} 接口联合多态求和案例2:
1、(拆分为 MyMath1类里面传多态) 2、(把所有东西,单独放进另一个 MyMath1类里面,然后进入这个类里面传多态,把这个 MyMath1类的mysum()方法当成main主方法)public class 匿名内部类之前案例 { public static void main(String[] args) { MyMath1 m = new MyMath1(); //Computer1 c1 = new ComputerImp(); //多态之后就可以通过c去找子类ComputerImp();的实现方法。因为接口全是抽象方法,无法使用。 //传方法的时候,实参声明变量可以随意的,只看中你传进来的实参。 m.mysum(100,200); //调用数学类的mysum方法,传实参。可以合并 m.mysum( new ComputerImp(),100,200); }}interface Computer1{ int sum(int a,int b );}class ComputerImp implements Computer1{ public int sum(int a,int b){ return a+b; }}class MyMath1{ //Computer c引用类型可以看做,数学类有个计算公式的接口, public void mysum(int x,int y){ //传形参(开始多态),注意这里的接口可以当成一个引用数据类型。 Computer1 c2 = new ComputerImp(); int result = c2.sum(x,y); //通过c1去找子类Comperterimp();的实现方法. System.out.println(x+"+"+y+"="+result);//System.out.println(c1.sum(x,y)); }} 上面例子的升级版:
1、在main方法new接口多态对象,连带接口对象一起传进去方法那里,然后直接调接口的方法即可,不用在mysum方法里面再new一次 2、但我觉得其实一样,看在那个地方new接口多态对象而已。public class 匿名内部类之前案例 { public static void main(String[] args) { MyMath1 m = new MyMath1(); Computer1 c1 = new ComputerImp(); //多态之后就可以通过c去找子类ComputerImp();的实现方法。因为接口全是抽象方法,无法使用。 //传方法的时候,实参声明变量可以随意的,只看中你传进来的实参。 m.mysum(c1,100,200); //调用数学类的mysum方法,传实参。可以合并 m.mysum( new ComputerImp(),100,200); }}interface Computer1{ int sum(int a,int b );}class ComputerImp implements Computer1{ public int sum(int a,int b){ return a+b; }}class MyMath1{ //Computer c引用类型可以看做,数学类有个计算公式的接口, public void mysum(Computer1 c2 ,int x,int y){ //传形参(开始多态),注意这里的接口可以当成一个引用数据类型。 int result = c2.sum(x,y); //通过c1去找子类Comperterimp();的实现方法. System.out.println(x+"+"+y+"="+result);//System.out.println(c1.sum(x,y)); }} 接口和多态联合案例2:
1、把一个类封装为另一个类的实例属性,去放进有参构造方法里的目的: 类套类,是为了使两个类产生联系,通过一个类引用可以进入另一个类里面访问其属性或者方法。(细品)/* //原来的思路 主:人(主动对象)+喂(方法)+宠物(被动对象), 如果最后被动对象食物没有继续多态,那么直接就在喂方法那里直接调吃的方法就行(体现多态),不用去测试类调. //升级版,现在主人不是直接在他的方法里面喂养宠物,而是下一个order命令,通过菜单接口,让仆人like一个菜单,去实现做菜去喂养宠物。 让仆人实现菜单喂养功能,仆人就像like一个喂养菜单给动物喂食*/public class 抽象类为喂宠物方法升级 { public static void main(String[] args) { foodMenu1 f1 = new MaleServant("男仆人"); Master m = new Master("zhangsan",f1); //使得主人和菜单产生联系。可以通过主人去调用菜单的喂养方法。 m.order(); //主人进入下命令方法,然后再进入菜单让仆人实现去喂养。 }}// 类;测试类,主人类,动物抽象类class Master{ //主人类。 String name ; foodMenu1 foodMenu; public Master() { } public Master(String name,foodMenu1 foodMenu) { this.name = name; this.foodMenu = foodMenu; } public void order(){ foodMenu.feedchongzi(new Bird("鸟儿")); foodMenu.feedpetLiangshi(new Dog("狗儿")); foodMenu.feedfish(new Cat1("猫儿")); }}interface foodMenu1{ void feedchongzi(Animal1 animal1); //虫子 void feedpetLiangshi(Animal1 animal2); //宠物粮食 void feedfish(Animal1 animal3); //鱼肉}class MaleServant implements foodMenu1{ //男仆人 String name; public MaleServant() { } public MaleServant(String name) { this.name = name; } public MaleServant(String name, foodMenu1 foodMenu) { this.name = name; } @Override public void feedchongzi(Animal1 animal1) { System.out.println("男仆人给"+animal1.getName()+"喂虫子"); animal1.eat(); } @Override public void feedpetLiangshi(Animal1 animal2) { System.out.println("男仆人给"+animal2.getName()+"喂宠物粮"); animal2.eat(); } @Override public void feedfish(Animal1 animal3) { System.out.println("男仆人给"+animal3.getName()+"喂鱼肉"); animal3.eat(); }}abstract class Animal1{ //抽象动物类 public abstract void eat();//抽象方法 public abstract String getName();}class Bird extends Animal1{ String name; public Bird() { } public Bird(String name) { this.name = name; } // public abstract void move();//非抽象类继承了抽象类,因此抽象类的抽象方法也会继承,但是子类却是非抽象类(不能放抽象方法),因此不能放继承过来的抽象方法,直接报错 public void eat() { //因此必须去掉abstract重写覆盖子类的抽象方法,实例化抽象方法。 System.out.println(this.name+"在吃虫子"); //可以和多态向上连用,面向抽象编程,不会固定死对象降低耦合度,提高扩展性 } public String getName(){ return "鸟儿"; }}class Dog extends Animal1{ String name; public Dog() { } public Dog(String name) { this.name = name; } public void eat() { //因此必须去掉abstract重写覆盖子类的抽象方法,实例化抽象方法。 System.out.println(this.name+"在吃宠物粮"); //可以和多态向上连用,面向抽象编程,不会固定死对象降低耦合度,提高扩展性 } public String getName(){ return "狗儿"; }}class Cat1 extends Animal1{ String name; public Cat1() { } public Cat1(String name) { this.name = name; } public void eat() { //因此必须去掉abstract重写覆盖子类的抽象方法,实例化抽象方法。 System.out.println(this.name+"在吃猫粮"); //可以和多态向上连用,面向抽象编程,不会固定死对象降低耦合度,提高扩展性 } public String getName(){ return "猫儿"; }}男仆人给鸟儿喂虫子鸟儿在吃虫子男仆人给狗儿喂宠物粮狗儿在吃宠物粮男仆人给猫儿喂鱼肉猫儿在吃猫粮 接口和多态联合案例3:
1、把一个类封装为另一个类的实例属性,去放进有参构造方法里的目的: 类套类,是为了使两个类产生联系,通过一个类引用可以进入另一个类里面访问其属性或者方法。(细品)2、具体开发步骤(重点必须掌握)? 顾客类“面向接口调用菜单方法” + 接口菜单(解耦提扩)+ 厨师类“实现接口菜单里的具体菜的方法”(各司其事)④学会在测试类中,间接创建接口和厨师类对象(前提有实现关系),(诀窍,谁去实现接口,就去new谁 FoodMenu f1 = new ChineseCook(); 厨师实现菜单接口,就去创建接口和厨师的多态对象)⑤ 学会将(封装接口为一个实例属性)FoodMenu foodMenu; ——》就可以去通过顾客类去“面向接口去调用”进入菜单里面菜名,完成顾客需要完成的点菜方法。⑥学会将厨师类去实现接口菜单。class AmericaCook implements FoodMenu——》即厨师like一个菜单实现了做菜功能” 3、具体案例;中午去饭店吃饭 1、定义一个接口,“菜单”就是一个接口(菜单上面有一个抽象的照片,番茄炒西红柿) 2、谁去面向接口“调用接口”?(前台顾客面向菜单点菜,是接口的调用者) , 3、谁去“实现接口”?(后台厨师负责做好(实现)接口菜单的菜,是接口的实现者) 4、总结;这个接口具体在饭店有什么用? “菜单接口”,其实就是将前台顾客和后台厨师解耦合了。这样顾客和厨师就能各司其职,不用牵一发而动全身。(耦低扩高) 顾客不用找厨师,厨师也不用找顾客。他们通过“菜单接口”来进行沟通。(顾客只需点菜单方法,厨师只需实现接口菜单里的具体菜的方法,各司其职)public class 接口在开发中的作用 { public static void main(String[] args) { FoodMenu f1 = new ChineseCook();//构造放一个类对象,通过一个厨师类去实现菜单接口,间接放接口。 //创建中国厨师对象。 “以后要改就只要改测试程序这里中餐变西餐即可,耦合度低,扩展性高,OCP” FoodMenu f1 = new AmericaCook(); Customer c = new Customer(f1); //创建顾客对象 ,在构造方法给菜单属性赋值,赋值一个中国厨师给菜单,相当于在这里实现了多态。 // 传new ChineseCook();一个中国厨师对象进去菜单实现多态,(就是厨师去菜单里面做菜)。 父FoodMenu foodMenu = new ChineseCook();子。此时foodMenu = f1; //或者直接传实参 Customer c = new Customer(new ChineseCook());// c.getFoodMenu().chichen(); // c.getFoodMenu().Fish();// order方法从java程序上就是为了拆分去具体变为某个功能,从而简化主方法的调用 c.order(); //进入点菜方法流程,①先拿菜单 ②进入菜单点具体菜。 }}interface FoodMenu{ //抽象接口菜单 void chichen(); // void Fish(); //}//完成实现接口的厨师类。class AmericaCook implements FoodMenu{ //后台”美国厨师“具体实现抽象菜单的菜 public void chichen(){ System.out.println("美国厨师做的炸鸡"); } public void Fish(){ System.out.println("美国厨师做的炸鱼"); }}class ChineseCook implements FoodMenu{ //后台”中国厨师“具体实现抽象菜单的菜 public void chichen() { System.out.println("中国厨师做的宫爆鸡丁"); } public void Fish() { System.out.println("中国厨师做的红烧鲤鱼"); }}//完成“面向接口调用”的顾客类。class Customer{ //前台顾客类 private FoodMenu foodMenu; // 这里表示,顾客手里has a 有个菜单 foodMenu即是一个引用也是一个实例变量。// ChineseCook cc; 如果下面直接让顾客和固定的厨师产生关系的话,就会直接写死(焊接死了,无法可插拔)。 顾客只能吃中餐// AmericaCook ac; 顾客只能吃西餐、//顾客只需完成下面的点菜方法即可(前提定义了接口实例属性,然后访问) public void order(){ //顾客点菜的方法(就是拿到菜单),有两种办法 这里 类似Address addr = a;两个指向的地址都是一样的,可以相等// FoodMenu fM = this.getFoodMenu(); //this相当于上面的c顾客引用。 //①私有可以调get方法,接收返回的foodMenu。(先拿到菜单)// fM.Fish(); //再用引用去去调放啊即可(进入菜单)// fM.chichen(); foodMenu.chichen(); //②,虽然是私有,但是在私有实例变量本类也可以直接引用名.来访问(常用) foodMenu.Fish(); //实际上执行到这里,虽然是静态编译去foodMenu父类接口调,但实际是会去子类cook1.动态编译,因为多态已经传了一个厨师进来。 } //有参构造已经把接口属性foodMenu赋值了cook1 ,因此foodMenu = f1 //这里是额外的私有接口属性构造 public Customer(){ } public Customer(FoodMenu foodMenu) { //传cook1间接为多态,FoodMenu foodMenu = f1,因此foodMenu = f1; this.foodMenu = foodMenu; //因此this.foodMenu = new ChineseCook(); ,这一步说明中国子厨师开始看父菜单实现做菜了 } public FoodMenu getFoodMenu() { //要学会封装代码的习惯,不要在外面点点点,要访问就掉get,要修改就掉set。 return foodMenu; } public void setFoodMenu(FoodMenu foodMenu) { this.foodMenu = foodMenu; }}中国厨师做的宫爆鸡丁中国厨师做的红烧鲤鱼 2、匿名内部类InnerClass
1、什么是内部类?
在类内部定义了一个新的类,这个类被称为内部类。例如在类中定义接口的新类。2、内部类分类?
静态、实例、局部(包含匿名内部类),(一般匿名内部类用最多)。3、什么是匿名内部类?
局部内部类的一种,直接(new 接口的方法)去定义接口的方法。4、匿名内部类作用?
【1】是实现接口的另一种形式。 【2】通俗讲:就是:可以不用再定义一个实现类去实现接口,直接在参数定义接口方法,去实现接口5、怎么才能去引出匿名内部类?(语法格式)
1、注意接口不能直接创建new对象,只能通过多态间接new 2、因此内部类就恰巧就不用多态创建对象。 原来:Computer1 c1 = new ComputerImp();3、使用了匿名内部类后:new+ 接口名+()+{}+原本去实现接口的方法。
现在: new Computer(){ //引出匿名类 public int sum(int a,int b){ return a+b; } } 4、总结:【1】使用了匿名内部类之后,可以少定义了一个ComputerImp()实现类从而减少一些内存,但是传参或者调用还是和原来的没区别的。(因此内部类纯属就是为了减少了一个实现类的定义而已)【2】我个人不推荐使用,因为你多写一个实现类不仅让自己思路更加清晰,而且还方便多态接口去切换别不同的实现类。但是你使用匿名内部类之后就写死了,无法让接口去重复使用。(淦!)
6、匿名内部类的优缺点? 【1】匿名内部类的优点:不用去定义实现类去创建多态接口对象,直接在接口后面+匿名内部类(在内部类里面写接口的实现方法)。 【2】匿名内部类的缺点:可读性很差,尽量少用。
因为匿名内部类没有类名,因此不能重复使用,类也无法被调用。一、内部类概述案例:
public class 内部类概述 { }class Test01{ static class Inner01{ //静态内部类 } class Inner02{ //实例内部类 } public void dosome(){ class Inner03{ // 局部内部类 } }} 二、static静态内部类概述:
� 静态内部类不会持有外部的类的引用,创建时可以不用创建外部类� 静态内部类可以访问外部的静态变量,如果访问外部类的成员变量必须通过外部类的实例访问【示例代码】public class InnerClassTest02 { static int a = 200;int b = 300;static class Inner2 { //在静态内部类中可以定义实例变量int i1 = 10;int i2 = 20;//可以定义静态变量static int i3 = 100;//可以直接使用外部类的静态变量static int i4 = a;//不能直接引用外部类的实例变量//int i5 = b;//采用外部类的引用可以取得成员变量的值int i5 = new InnerClassTest02().b;}public static void main(String[] args) { InnerClassTest02.Inner2 inner = new InnerClassTest02.Inner2();System.out.println(inner.i1);}} 三、实例内部类概述:
创建实例内部类,外部类的实例必须已经创建� 实例内部类会持有外部类的引用� 实例内部不能定义 static 成员,只能定义实例成员public class InnerClassTest01 { private int a;private int b;InnerClassTest01(int a, int b) { this.a = a;this.b = b;}//内部类可以使用 private 和 protected 修饰private class Inner1 { int i1 = 0;int i2 = 1;int i3 = a;int i4 = b;//实例内部类不能采用 static 声明//static int i5 = 20;}public static void main(String[] args) { InnerClassTest01.Inner1 inner1 = new InnerClassTest01(100, 200).new Inner1();System.out.println(inner1.i1);System.out.println(inner1.i2);System.out.println(inner1.i3);System.out.println(inner1.i4);}} 四、局部内部类概述:
局部内部类是在方法中定义的,它只能在当前方法中使用。和局部变量的作用一样局部内部类和实例内部类一致,不能包含静态成员public class InnerClassTest03 { private int a = 100;//局部变量,在内部类中使用必须采用 final 修饰public void method1(final int temp) { class Inner3 { int i1 = 10;//可以访问外部类的成员变量int i2 = a;int i3 = temp;}//使用内部类Inner3 inner3 = new Inner3();System.out.println(inner3.i1);System.out.println(inner3.i3);}public static void main(String[] args) { InnerClassTest03 innerClassTest03 = new InnerClassTest03();innerClassTest03.method1(300);}} 五、不用匿名内部类的案例?(匿名内部类属于局部内部类)
public class 匿名内部类之前案例 { public static void main(String[] args) { MyMath1 m = new MyMath1(); Computer1 c1 = new ComputerImp(); //多态之后就可以通过c去找子类ComputerImp();的实现方法。因为接口全是抽象方法,无法使用。 //传方法的时候,实参声明变量可以随意的,只看中你传进来的实参。 m.mysum(c1,100,200); //调用数学类的mysum方法,传实参。可以合并 m.mysum( new ComputerImp(),100,200); }}interface Computer1{ int sum(int a,int b );}class ComputerImp implements Computer1{ public int sum(int a,int b){ return a+b; }}class MyMath1{ //Computer c引用类型可以看做,数学类有个计算公式的接口, public void mysum(Computer1 c2 ,int x,int y){ //传形参(开始多态),注意这里的接口可以当成一个引用数据类型。 int result = c2.sum(x,y); //通过c1去找子类Comperterimp();的实现方法. System.out.println(x+"+"+y+"="+result);//System.out.println(c1.sum(x,y)); }} 使用匿名内部类后的效果?
public class 匿名内部类案例 { public static void main(String[] args) { MyMath m = new MyMath(); // Computer c1 = new ComputerImp(); //多态之后就可以通过c去找子类ComputerImp();的实现方法。因为接口全是抽象方法,无法使用。 m.mysum( new Computer(){ //引出匿名类 public int sum(int a,int b){ return a+b; } },100,200); //调用数学类的mysum方法,传实参。可以合并 m.mysum( new ComputerImp(),100,200); }}interface Computer{ int sum(int a,int b );}/*class ComputerImp implements Computer{ public int sum(int a,int b){ return a+b; }}*/class MyMath{ //Computer c引用类型可以看做,数学类有个计算公式的接口, public void mysum(Computer c ,int x,int y){ //传形参,注意这里的接口可以当成一个引用数据类型实例。 int result = c.sum(x,y); //通过c1去找子类Comperterimp();的实现方法. System.out.println(x+"+"+y+"="+result);//System.out.println(c1.sum(x,y)); }} 3、包package和导包import
一、包(关键字:package):
1、包概念:相当于是一个文件夹目录,特别是项目比较大,java 文件特别多的情况下,我们应该分目录管理,在java 中称为分包管理。 2、包作用:为了方便java文件的管理,不同功能的类放在不同的包中(通常按照功能划分,) 3、包语法结构;package+包名 比如:package com.bjpowernode.javaSE.Object类; //说明你这个java文件是在这个包下面去编写的 ①包名最好采用小写字母 ②包的命名有一定的规则,不能重复,一般采用: 公司网址倒序.项目名称.模块名称 //com.bjpowernode.exam.Object类 4、package关键字必须放到 所有语句的第一行,注释除外package com.bjpowernode.exam.Object类;public class PackageTest01 { public static void main(String[] args) { System.out.println("Hello Package!!!");}} 二、导包(关键字:import)
1、import导包机制结构? ①出现位置; 【1】只能出现在class之上,package之下。 【2】idea出现灰色字的import就两种情况:一是在同一个包下不需要import导包,二是没有创建到该import所导入的类的对象默认你没用。②语法结构;
import+包名+类名; import com.bjpowernode.javaSE.Object类.package使用例子; (正常) import com.bjpowernode.javaSE.Object类.*; (懒人) //加 *代表全部导入,是通配符号2、使用import机制有什么用?
【1】当你需要使用到其他包中的类时,import可以提前导入其他包中的类,编写程序中则可以去除程序包名,之后就可以直接和原来一样用new类名.访问【2】日常开发中很常见import,因为java软件有很多包和类都是sun公司提前写好给我程序员使用的,因此当我们想要在自己的自定义包中的类下,去使用sun已写好的某个包下的类去完成某个功能时,就可以直接import导包把sun内置的类拿过来为我们所用。(秒啊!)
比如:
原来:new对象要包+类名; com.bjpowernode.javaSE.Object类.package使用例子 p2 = new com.bjpowernode.javaSE.Object类.package使用例子(); 现在:new对象只要类名 import com.bjpowernode.javaSE.Object类; package使用例子 p1 = new package使用例子();3、总结;import和package
①package没有任何实际功能,仅仅只是说明程序在该包内编写,方便程序员管理和分辨而已。 ②import(前提是有包机制存在了,eclipase和IDEA就是有包和导包机制) 【1】如果当前包中的类要new 其他包中类的对象,并且两个类不在同一包中,则需要使用import,提前导入其他包的包+类名,在程序中则可以去除程序包名(最常用!) 【2】如果A、B两个类在同一包中,则不需要使用import,直接在A类中使用(新建)B类对象。1、现在可以解释之前学的Scanner为什么new这么长!
①因为在原来的EditPlus没使用import导包机制!!! java.util.Scanner s = new java.util.Scanner(System.in);②而现在的Eclipase和IDEA就是有包和导包机制
import java.util.Scanner; Scanner s2 = new Scanner (System.in);/*先解释这个Scanner用户输入模式的原理:哈哈,跟我当年一样,刚学的时候我也好奇,老师也没讲,现在我告诉你Scanner 是一个类,in是一个实例或者说是对象!new 是一个创建对象的方法……Scanner这个类最实用的地方表现在获取控制台输入就相当与声明这是一个人类(Scanner),这个人类是谁(in),后面新创建一个人类new Scanner(system.in),system.in 表示他有什么特征。总的来说就是新创建一个输入的Scanner 对象,然后赋值给in。其实只要 知道 他的作用就是获取控制台的输入就行了!! */package com.bjpowernode05javaSE.Object类;public class 解释Scanner { public static void main(String[] args) { System.out.println("欢迎使用本系统,请你输入字符串"); java.util.Scanner s = new java.util.Scanner(System.in); //没使用import java.util.Scanner;导包 Scanner s2 = new Scanner (System.in); //使用import java.util.Scanner; String str = s.next(); //调用next方法之后,接收返回值. System.out.println("您输入的字符串是"+ str); //输出返回值 System.out.println("您输入的字符串是"+ s.next()); //直接输出法 }} 对比下面使用import导包机制后:
import java.util.Scanner; Scanner s2 = new Scanner (System.in);package com.bjpowernode05javaSE.Object类;import java.util.Scanner;public class 导入Scanner包名 { public static void main(String[] args) { System.out.println("你好皮皮鳝,欢迎使用本打飞机系统,请你输入列夫和皮皮鳝的小弟弟长度数字"); Scanner s = new Scanner(System.in); //使用了import java.util.Scanner;导包 Scanner s2 = new Scanner (System.in); //使用import java.util.Scanner; int x = s.nextInt(); //调用next方法之后,接收返回值. int y = s.nextInt(); System.out.println(x>y ? x :y); //三元运算符 }} 4、Object类(API)
一、先了解API
1、API官方概念: 【1】API(Application Programming Interface,应用程序编程接口)是一些预先定义的函数,目的是提供应用程序与开发人员基于某软件或硬件的以访问一组例程的能力,而又无需访问源码,或理解内部工作机制的细节。 【2】API除了有应用“应用程序接口”的意思外,还特指 API的说明文档,也称为帮助文档。 2、API通俗概念: 【1】当我们做某一类型事情的时候,不会做,就会去寻找相应的解决办法,方法在哪里?就是API帮助文档?(jdk api 1.8_google.CHM) 【2】从API我们能看到一个类的继承关系 以及 实现的接口 【3】要API学习的内容:主要学习三个包: ① lang包 : Object,String,System类,Number数字类(包装类) ②util包 : Array工具类(最多是排序和二分法查找), Collection,List,Set,Map集合类, Random类(此类的实例用于生成伪随机数流) ③IO包 : FileInputStream ,FileOutputStream 输出输入流3、API帮助文档的内容及作用:
①是一些预先定义的函数,目的是提供应用程序与开发人员基于某软件或硬件的以访问一组例程的能力,而又无需访问源码,或理解内部工作机制的细节。 ②运行Java程序时,虚拟机装载程序的class文件所使用的就是Java API class文件。 所有被装载的class文件 (包括从应用程序中和从Java API中提取的) 和所有已经装载的动态库(包含本地方法) 共同组成了在Java 虚拟机上运行的整个程序。 ③在一个平台能够支持Java程序之前,必须在这个特定平台上明确地实现API的功能。为访问主机上的本地资源,Java API调用了本地方法。由于Java API class文件调用了本地方法,Java程序就不需要再调用它们了。通过这种方法,Java API class文件为底层主机提供了具有平台无关性、标准接口的Java程序。 ④对Java程序而言,无论平台内部如何,Java API都会有同样的表现和可预测的行为。正是由于在每个特定的主机平台上明确地实现了Java虚拟机和Java API, 因此,Java程序自身就能够成为具有平台无关性的程序。4、切记我们程序员是面向接口编程的, 因此很多时候都是写一个自定类去实现sun写好的接口,然后就能实现和使用里面的方法了。我们很多时候都是无需自己定义接口,只需要编写实现子类,就能拿API接口过来用了
二、开始学习API中的Object类
1、Object 类是所有 Java 类的根基类(老祖宗) 2、 如果在类的声明中未使用 extends 关键字指明其基类,则默认基类为 Object 类 如: public class User { } 相当于默认等于public class User extends Object {
} 3、再看看实际src源码(看要学些什么类方法):public class Object { private static native void registerNatives(); static { registerNatives(); //当源码方法以分号结尾,并且带有“native”,关键字,表示底层调用的是c++的dll程序的动态链接库文件 } public final native Class getClass(); public native int hashCode(); // int hashCode方法 ,底层也是c++ ,获取对象哈希值的一个方法 public boolean equals(Object obj) { //equals方法, boolean equals (Object obj){} 方法 //判断两个对象是否相等的方法 return (this == obj); } protected native Object clone() throws CloneNotSupportedException; //clone方法,克隆对象。底层也是调用的c++ public String toString() { //toString方法,toString就是把对象转换为String字符串的方法 return getClass().getName() + "@" + Integer.toHexString(hashCode()); } //String toString(){} 方法 //将对象(也就是引用名地址)转换为字符串形式 public final native void notify(); //多线程方法 public final native void notifyAll();//多线程方法 public final native void wait(long timeout) throws InterruptedException;//多线程方法 public final void wait(long timeout, int nanos) throws InterruptedException { //多线程方法 if (timeout < 0) { throw new IllegalArgumentException("timeout value is negative"); } if (nanos < 0 || nanos > 999999) { throw new IllegalArgumentException( "nanosecond timeout value out of range"); } if (nanos > 0) { timeout++; } wait(timeout); } public final void wait() throws InterruptedException { //多线程方法 wait(0); } protected void finalize() throws Throwable { } //protected void finalize(){} 方法 ,垃圾回收器负责调用的方法} 2、但实际我们只需要学Object类中以下几个方法即可.
①String toString(){} 方法 //将对象(也就是引用名地址)转换为具体字符串形式。②boolean equals (Object obj){} 方法 //判断两个对象具体内容是否相等的方法③int hashCode(){}方法 //获取对象哈希值的一个方法,切记不是对象内存地址!④protected Object clone(){} 方法 // 负责对象克隆的方法⑤protected void finalize(){} 方法 //垃圾回收器负责调用的方法⑥notify()/notifyAll()/wait() //这三个都是多线程方法,很后面多线程再讲 3、以后开发注意的习惯:
老祖宗Object类(toString方法、equals方法)、自定义类(要自己重写)、String类(sun已帮我们重写好方法);
①Object类是是所有类的老祖宗类, 包括String类也是其子类,类里面有各种方法(包括toString方法、equals方法) ②以后所有的自定义类的toString方法都需要重写。(防止要用“引用”或者调用该方法输出对象的属性的)。 System.out.println(s1);/System.out.println(s1.toString()); ③以后所有的自定义类的equals方法也需要重写。(防止要比较两个对象是否相等的)。 System.out.println(s3.equals(s4)); ④而String类是Sun公司已经写好内置的,(包括toString方法、equals方法都已经帮你重写好了)`
【1】toString方法:(返回String类型)
1、通常 toString 方法会返回一个“以文本方式表示”此对象的字符串,Object 类的 toString 方法返回一个字符串,该字符串由类名加标记@和此对象哈希码的无符号十六进制表示组成(但输出的格式不友好,因此无法看懂) ①Object 类 toString 源代码如下: getClass().getName() + ‘@’ + Integer.toHexString(hashCode()) ②重写之后(IDEA内置写法)public String toString() { return "Test02{" +"year=" + year + ", month=" + month + ", day=" + day + '}'; ③也可以自动定规则重写,但要注意:
一定要部分或者全部带有字符串类型形式。 return this.year + this.month + this.day; 这样就会报错。里面只有int类型public String toString() { //重写toString方法。 return this.year +"年"+ this.month+"月" + this.day+"日"; } 2、注意:sout输出对象的引用,他会自动调toString方法,然后输出的。 (下面两者一样)
System.out.println(t2); //2020年9月8日 System.out.println(t2.toString());//2020年9月8日3、toString方法使用案例展示:
public class Object中的toString方法 { //早没有显示继承的关系下,默认都是继承Object public static void main(String[]args) { //这里是Test01不重写toString方法之后的情况 Test01 t1 = new Test01(1999,11,11); //继承了object所有方法 System.out.println(t1); //这里JVM默认会去调用Object的toString方法的 // Test01@15db9742 ,因为没有重写toString方法,直接输出引用的是一个对象内存地址, System.out.println(t1.toString()); //也是Test01@15db9742,返回的是一个哈希算法的十六进制的数值结果 //上面3个相同的结果,说明输对象引用,他会自动调toString方法的地址,然后输出。之前的引用也是输出之后默认调的是toString方法的地址 //这里是Test02重写toString方法之后的情况,可以将直接输出引用地址变为返回具体实参。不用再用引用.属性名方式访问 Test02 t2 = new Test02(2020,9,8); System.out.println(t2); //2020年9月8日 System.out.println(t2.toString());//2020年9月8日 }}class Test01 extends Object{ //没有显示继承的关系下,默认都是继承Object类,包括其中的toString方法 int year; int month; int day; public Test01(){ } public Test01(int year, int month, int day) { this.year = year; this.month = month; this.day = day; }}class Test02 extends Object{ //没有显示继承的关系下,默认都是继承Object类,包括其中的toString方法 int year; int month; int day; public Test02(){ } public Test02(int year, int month, int day) { this.year = year; this.month = month; this.day = day; } @Override public String toString() { //重写toString方法。 return this.year +"年"+ this.month+"月" + this.day+"日"; //一定要带有字符串类型形式。 } // return this.year + this.month + this.day; 会报错。里面只有int } 【2】Object中的equals方法:返回boolean类型 (超级重要!)
(推荐直接用IDEA 自动生成的equals方法,节约开发时间,但是原理和源代码一定要看懂)1、自己重写+IDEA的各种equals方法解析和原理:
import java.util.Objects;public class Object中的equals方法 { public static void main(String[] args) { int a = 100; int b = 100; System.out.println(a==b);//比较基本数据类型大小,直接用 ==号 true Mytime t1 = new Mytime(2020,1,1); Mytime t2 = new Mytime(2020,1,1); System.out.println(t1 == t2); //false,虽然两个对象内容一样,但是结果却是false //因为双等号只能比较对象当中的地址,所以两个对象是完全不同的对象,自然地址也不同。就是false //因此 要用 equals方法来比较的是引用数据类型的对象具体内容属性是否相等。 //Mytime t2 = new Mytime(); 前提有继承。 boolean flag= t1.equals(t2);//调用t1继承的equals方法。 t2传进去相当于相当于多态 Object obj = new Mytime(); ,然后接收布尔类型的返回值。 //此时 equals方法的this为t1,obj为t2. 因此最后结果还是 t1==t2. 还是false //总结,比较对象大小时,必须重写父类Object的equals方法,Object类的equals方法不能满足(老祖宗只能比较对象地址,不能比较对象具体内容)。 System.out.println(flag); // true,重写之后两个对象相等。 }}class Mytime{ //默认继承Object老祖宗类 int year; int month; int day; public Mytime(int year, int month, int day) { this.year = year; this.month = month; this.day = day; }// public boolean equals(Object obj) { //这里是没有重写equals方法之前,默认继承父类Object的equals方法// return (this == obj);// } public boolean equals(Object obj){ //这里为什么放Object这样不会写死,任何对象都能放进来,向上多态。 //t2传进去相当于相当于多态 Object obj = new Mytime(); ,t2参数没啥用的,后面传的对象才有用。 //怎么重写?(比较地址的具体内容,当年相同,月相同,日相同的时候,说明两个对象相等) //获取第一个日期的年月日 //获取第二个日期的年月日 //开始比对//自己设计的效率不高的equals方法 /* int year1 = this.year; //获取第一个日期的年月日 int month1 = this.month; int day1 = this.day; if (obj instanceof Mytime){ Mytime m=(Mytime)obj; int year2 = m.year; //获取第二个日期的年月日, 第二个日期参数多态的时候必须向下转型,因为Object类没有年月日三个属性,因此调用的是子类特有的东西,必须得向下转型。 int month2 = m.month; int day2 = m.day; return year1 == year2 && month1==month2 && day1 == day2 ; //这种考虑不全面,而且会出现空指针异常bug,就是对象一开始就为空Mytime t2=null,调方法传过去给了obj为null //则(obj instanceof Mytime)中的 obj父类对象也为 null, 父类直接无法强转为子类,直接输出false。 }else{ return false; } *///自己设计的改良equals方法。 if (obj == null ||!( obj instanceof Mytime)){ //如果前面传的对象给obj就为null空时,直接false,不用比了。 return false; //或者如果obj不是一个Mytime的话也不用比下去了,无法强转不了。 } if(this == obj){ //如果一开始this和obj的内存地址就一样,说明是相同对象了,例如对象相同 t1.equals(t1); 则不用比了,一开始就地址一样,对象内容肯定相等。 return true; } //程序排除上面的之后,执行到这里说明,Obj肯定是Mytime类型,不用再加判断就可以开始强转了。 Mytime m=(Mytime)obj; //这里的m,其实是t2传进去向上多态转型obj之后,再向下强转的m。其实m间接继承了t2。 //为什么要强转?因为一开始是向上多态 Object obj = new Mytime(); ,是一个Object类型,因此要强转为Mytime //执行到这里,两个对象都为Mytime了,开始比较里面具体内容即可。 return this.year == m.year && this.month == m.month && this.day==m.day; //相等结果为true。 }IDEA 自动生成的equals方法(推荐直接用,节约开发时间,但是原理和源代码一定要看懂) @Override public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; Mytime mytime = (Mytime) o; return year == mytime.year && month == mytime.month && day == mytime.day; }} 2、综合案例类套类套娃equals方法:
①如果User对象类中包含有一个Address的套娃引用类,则两个类的equals方法都要重写。因为比较user两个对象之前,得确保也把包含在User里面的Adress引用类型也得相等。②因此重写equals方法必须得彻底,只要有引用类型都要重写equals。(包括类套类产生联系,则两个类都需要重写equals)
例如class User{ String name; //String引用类型都用equals方法 Address addr; //套用Address引用类型比较也要用equals方法} 比较user两个对象之前,得先也里面的Adress引用类型也得先比较出来。import java.util.Objects;public class Object中的equals方法综合案例 { public static void main(String[] args) { Address a1 = new Address("广州市","永兴街","12346"); //可以在外面new好对象赋值先,也可以在User里面放a1,a2或者直接放new赋值的对象。 Address a2 = new Address("广州市","永兴街","12346"); User u1 = new User("tuyuexin",new Address("广州市","永兴街","12346")); User u2 = new User("tuyuexin",a2);// System.out.println(u1.equals(u2)); //这里为false不相等,因为Adress引用类的equals方法没有重写,因此this.addr和u.addr比较的是两个对象的内存地址 //两个new的Adress内存地址肯定是不相等的,因此u1和u2也会不相等。 //解决方法,再次重写Address引用类的equals方法。 System.out.println(u1.equals(u2));// 这里为true,重写Adress引用类的equals方法后,就可以判断 name和Adress两个内容完全相等了 }}class User{ String name; //String引用类型都用equals方法 Address addr; //Adress引用类型比较也要用equals方法 public User(){ } public User(String name, Address addr) { //构造方法,赋值name和addr this.name = name; this.addr = addr; } //重写equals方法比较user类的对象大小 public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; User u = (User) o;//这里的u,其实是u2传进去向上多态转型o之后,再向下强转的u。其实u间接继承了u2 return this.name.equals(u.name) && this.addr.equals(u.addr); //这里不是递归,而是引用类型必须要再次用equals比较,而String的equals方法源代码已写好,addr自己写好的。 }}class Address{ String city; String stress; String zipcode; public Address(){ } public Address(String city, String stress, String zipcode) { //构造方法,赋值city,stress,zipcode this.city = city; this.stress = stress; this.zipcode = zipcode; } @Override public boolean equals(Object o) { if (this == o) return true; if (o == null || getClass() != o.getClass()) return false; Address a = (Address) o; //这里的a,其实是a1传进去向上多态转型o之后,再向下强转的a。其实a间接继承了a2. return this.city == a.city && this.stress == a.stress && this.zipcode ==a.zipcode; } } 3、总结“==”和equals方法的区别?(面试题)
① ==等号是可以比较基本类型和引用类型的,但等号比较的是值,对于基本数据类型比较的具体数据字面值, 而比较引用类型,比较的是引用的内存地址(也是哈希码16进制值)
②equals方法比较的是引用数据类型的对象(包括new的String引用类型)内存地址的具体属性的内容是否相等。 ③总结:因为两个引用新建对象的内存地址是肯定不相同,各有各的堆内存地址,因此= =号是无法比较对象是否相等,只能用equals方法比较地址内的具体属性内容是否相等。(equals只要内容属性相等就true相等,不管对象的书写形式)
4、但有一个超极特殊的对象类String,两者都能用。
String类型是特殊的对象类 ,既可以用= =号可以用equals 但有条件限制的。 【1】先回顾一下: Java中“==” 双等号(关系运算符)比较的是一个值,比如基本数据类型变量的字面值 和 对象的内存地址哈希值(输出的true/false), 而equals方法比较的是引用对象的具体内容的属性(包括String引用类型)是否相等。(只要内容属性相等就相等,不管形式)(return true/false)【2】String特殊在于:String字符串在方法区常量池一旦创建就无法被改变(类似final修饰后的常量),
因此字符串字面值如果是相同的话就会多次被指向一个相同的方法区内存地址, 要改变指向只能重新再创建一个别的字面值的字符串。【3】案例String 中使用 = = 和 equals的案例?
①String s3=“abc”; 和String s4=“abc”; 【这里只有一个内存地址】 这里只比较的一个相同方法区地址值,因为对于String字符串字面值如果是相同的话就会多次被指向一个相同的方法区常量池内存地址, 因此此时可以用 ==号去比较内存地址值,但也可以调用String类已经重写好父类Object类的equals方法(equals更方便快捷)②String s3 = new String(“abc”);和 String s4 = new String(“abc”);
【这里一共有三个内存地址】 这里比较的的对象地址是,两个堆内存地址和一个方法区内存地址, 因为两个new String类对象会在堆内存会变为两个不同的地址了,而方法区内存常量池的地址中还是只有一个abc。 因此综上所述,此时是不能用==号, 必须只能调用String类已经重写好父类Object类的equals方法。③总结,最好比较任何引用对象大小都用equals方法比较。(省去很多麻烦事,但了解一下是必须的)
public class SUN公司String类已经重写好了Object类中的toString和equals方法 { public static void main(String[] args) { String s1 = "abc"; //一个内存地址 String s2 = "abc"; String s3 = new String("abc"); //两个内存地址 String s4 = new String("abc"); String s6 = "Hello"; //(equals就是用来判断地址具体内容是否一样的) String s7 = "World"; String s8 = "HelloWorld"; String s9 = "Hello" + "World"; String s10 = s6+s7; System.out.println(s1 == s2); //结果为true, System.out.println(s1.equals(s2)); //结果也为true, System.out.println(s3==s4); //结果为false, System.out.println(s3.equals(s4)); //true System.out.println(s1==s3);//false System.out.println(s1.equals(s3));//true 比较的具体对象内容 System.out.println(s2.equals(s4));//true 比较的具体对象内容 System.out.println(s8 ==s6 +s7);//false, s8保存的常量池地址和(s6+s7)保存的常量池地址肯定不一样,直接false 0x1111== 0x222+0x333 比较的地址肯定不相等 System.out.println(s8 ==s10);//false 一样false,和上面一样 System.out.println(s8 == s9);//true //如果一定是想要引用名相加 s6+s7, 必须则先创建具体内容字符串的合体空间,再拼接;例如s9 System.out.println(s8=="Hello"+"World");//true。常量名相加 "en"+"joy",则可以先拼接,然后在常量池中找拼接体,如果有不用再次创建,否则创建; System.out.println(s8.equals(s6+s7));//true,因为用equals去比两个不同地址里面的具体属性内容来判断是否相等。内容"HelloWorld"= "Hello"+"World"的确相等。 System.out.println(s8.equals("Hello"+"World"));//true String s5 = new String("广外南国商学院fat man");//SUN公司String类已经重写好了toString和equals方法,直接调用equals方法或者也可以不用引用也能直接访问了。 System.out.println(s5.toString());//经过测试可以直接输出结果,说明String已经重写了toString方法。 //如果String类没有重写toString方法,则这里就会输出,java.lang.String@十六进制地址。 System.out.println(s5);//重写了toString可以直接用引用调,会自动调toString方法,结果是一样的。 }} 【3】clone方法(了解也很重要):
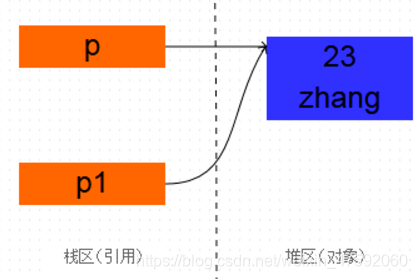
看着两位的博客先: 复制对象 VS 复制引用 区别? 深拷贝 VS 浅拷贝区别?Person p = new Person(23, "zhang"); Person p1 = p; //复制引用 System.out.println(p); System.out.println(p1);当Person p1 = p;执行之后, 是创建了一个新的对象吗? 首先看打印结果:com.pansoft.zhangjg.testclone.Person@2f9ee1accom.pansoft.zhangjg.testclone.Person@2f9ee1ac 说明并不是复制克隆了新对象,只是复制了引用,两个引用去指向同一个堆内存对象地址。
Person p = new Person(23, "zhang"); Person p1 = (Person) p.clone(); //克隆复制出新对象//因为clone返回的是一个Object类型,又因为Person是默认继承的Object,因此要强转才能接收返回值为person类型 System.out.println(p); System.out.println(p1); 打印出:com.pansoft.zhangjg.testclone.Person@2f9ee1accom.pansoft.zhangjg.testclone.Person@67f1fba0这说明才是克隆出一个一摸一样的新对象,而不是复制引用。
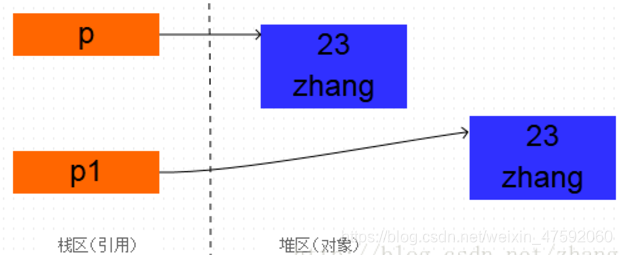
1、clone顾名思义就是克隆复制, 在Java语言中, clone方法被对象调用,所以会复制对象。所谓的复制对象,不是指复制引用去指向同一个堆内存地址,而是首先要分配一个和源对象同样大小的新空间,在这个新空间中创建一个新的对象。那么在java语言中,有几种方式可以创建对象呢?
【1】 使用new操作符创建一个新对象 【2】使用clone方法在原对象基础上再复制一个新对象【4】hashCode方法(了解,后面HashMap集合这个很重要,判断是否为哈希冲突的重要方法,接着会使用拉链法解决形成哈希表数据结构):
1、源代码 public native int hashCode(); // int hashCode方法 ,底层也是c++ ,获取对象哈希值的一个方法 2、用哈希值储存数据可以降低寻找数据的时间复杂度降为常数级。 3、hashCode()方法:hash哈希码(由key经过重写好的hashCode方法转为hash值)。public class Object类中的hashCode方法 { public static void main(String[] args) { Object o = new Object(); int i = o.hashCode(); System.out.println(i);//356573597,老祖宗Object对象的哈希值 Myclass mm = new Myclass(); System.out.println(mm.hashCode());//1735600054 System.out.println(mm); //Myclass@677327b6 对象内存地址 不等于 1735600054哈希值 不要弄混 }} 【5】finalize方法(了解):
1、finalize的src源代码 protected void finalize() throws Throwable { } //protected void finalize(){} 方法 ,垃圾回收器负责调用的方法 2、 finalize()方法只有方法体,里面没有代码内容,而且这个方法是protected修饰的。 3、finalize()方法不用程序员手动调用,JVM垃圾回收器会(Garbage Collection)自动负责调用这个方法。 4、finalize()方法只需要去重写即可,不需要调用 不像toString、equals是需要重写并且自己调用的。 5、finalize()方法执行时机(作用)?(回收类对象) 当一个java类对象即将被垃圾回收器回收的时候,垃圾回收器会自动调用该方法。 6、finalize()方法其实是sun公司给程序员提供的一个垃圾回收时机,如果希望对象销毁时执行一段代码,则需要用到finalize()方法 static{}静态代码块是sun公司为程序员提供的一个类加载时机,在类加载之前提供一段代码,并且只执行一次。public class Object中的finalize方法 { public static void main(String[] args) { Person p1 = new Person(); p1 = null; //p1为null的时候就会释放内存了,垃圾回收器就会回收person对象,就会去自己调用p.finalize();方法,回收Person对象 for(int i = 1;i<1000;i++) { Person p2 = new Person(); p2 = null; if (i % 2 == 0){ System.gc();//垃圾回收器手动启动器。 System.gc(); 不一定成功 } } } }class Person{ int age; //当Person类型对象被垃圾回收器回收的时候,垃圾回收器会自己负责调用p.finalize(); @Override protected void finalize() throws Throwable { super.finalize(); }} 转载地址:http://ppke.baihongyu.com/